数据库Chap2关系模型+Chap6关系代数
#sql
2023-11-20
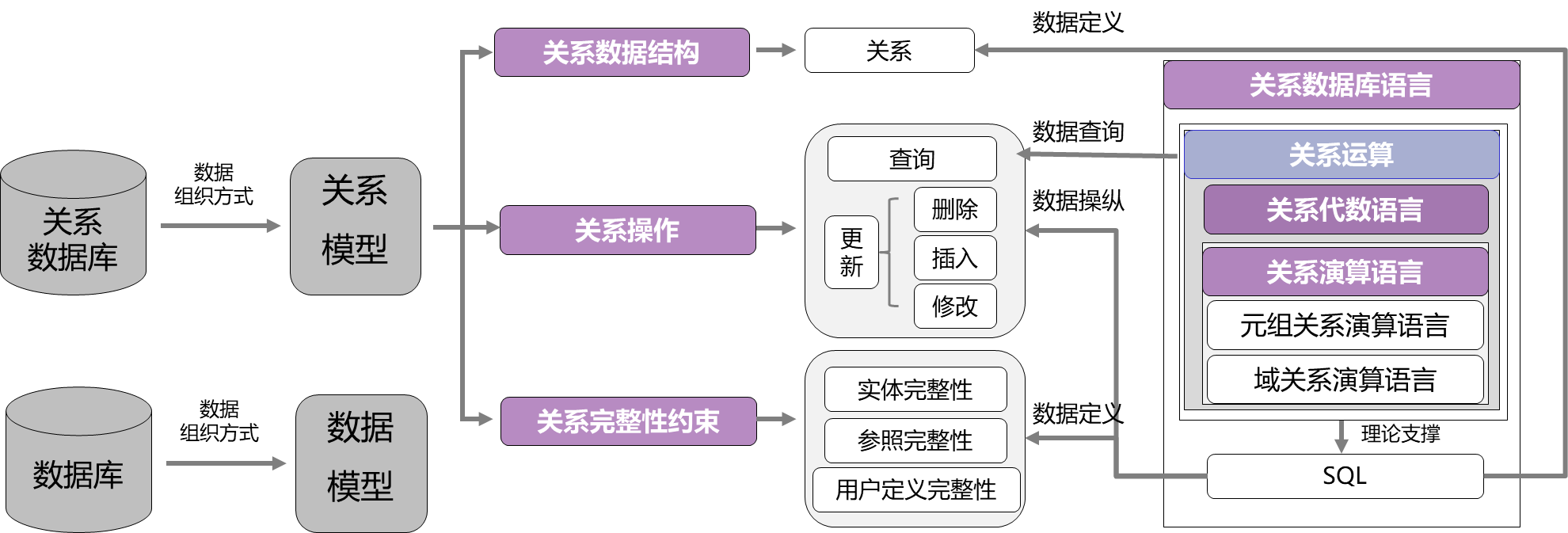
知识框架
目录:
Chap2 关系模型介绍
关系数据结构
关系数据库
- 关系数据库
- 关系数据库是表的集合:
- 每个表有唯一的名字
- 每个表可以有多个列
- 每个列有唯一的名字
- 表中的一行代表的是一系列值之间的联系,即表是关系的集合
- 表的概念和数学上关系的概念密切相关,这正是关系数据库名称的由来
- 关系数据库是表的集合:
- 常见的关系数据库
- Oracle 、Microsoft SQL Server、IBM DB2、 GaussDB、MySQL、SQLite
- 关系数据库采用关系模型作为数据的组织方式
关系模型
关系模型的形象化类比:
| 程序设计语言 | 关系模型 |
|---|---|
| - 数据类型 | - 关系模式 |
| - 变量 | - 关系 |
| - 值 | - 关系实例 |
关系模型术语
| 关系模型术语 | 一般表格术语 |
|---|---|
| 关系模式 | 表头(表格列名的集合) |
| 关系名 | 表名 |
| 关系relation | (二维)表 |
| 元组tuple | 行/记录 |
| 属性attribute | 列;属性中的值都应该来自同一个域 |
| 属性名 | 列名 |
| 属性值 | 列值 |
| 分量 | 一条记录中的一个列值,元组的一个属性值 |
| 域 | 关系的每个属性允许取值的范围 |
| 超键 | 能够唯一标识关系中的元组(每个元组都有一个唯一的标识符)的一个或多个属性集合。 |
| 候选键 | 不含有多余属性的超键:一个超键去除任意一个属性就不再是超键了。唯一标识关系(表)中的每个元组的属性或属性集合。候选键中的每个属性都是必需的,不能去掉其中任何一个属性。 |
| 主属性 | 候选键的各个属性称为主属性,不包含在任何侯选键中的属性称为非主属性。 |
| 复合键 | 在某些情况,需要同时使用两个或者两个以上的属性才能唯一标识不同的元组,这种由多个属性所构成的键称为复合键。(当单个属性都不能唯一的标识不同元组时) |
| 主键 | 一个关系可能有一个或多个候选键,在定义关系数据库关系表的时候,一般选择一个最合适的候选键作为主键,主键的不同取值必须唯一标识不同的元组。 |
| 外键 | SC关系的Sno和Cno属性分别是Student和Course关系的主键,这种一个关系模式R1中的属性是另一个关系模式R2的主键,这样的属性在R1上称作参照R2的外键,即外键。 |
| 空值 |
- Student关系的5个属性中,(Sno, Sname)是一个超键,但不是候选键;Sno是候选键;
- 如果Sname属性的取值是唯一的,则它也是候选键。
- Student关系主属性是Sno。
| Sno (学号) | Sname (姓名) | Sgender (性别) | Sage (年龄) | Sdept (所在系) |
|---|---|---|---|---|
| 2021310721 | 李博 | 男 | 17 | CS |
| 2021310722 | 赵宇 | 男 | 19 | CS |
| 2021310723 | 张敏 | 女 | 18 | CS |
| 2021310724 | 王勇 | 男 | 18 | MA |
| 2021310725 | 刘佳 | 女 | 17 | MA |
关系模式
- 关系模式是对关系的描述,由关系名和其属性集合组成,是相对不变的。记做R(A1, A2, ⋯, An)。
- Student关系可以写为Student(Sno, Sname, Sgender, Sage, Sdept)
关系实例
- 关系实例是关系元组集合,表示特定实例,会根据业务状态发生变化。
- Student关系的实例有5个元组,对应5个学生。如果有新学生,则其元组数会增加。
关系操作
- 增
- 删
- 改
- 查 --- 核心
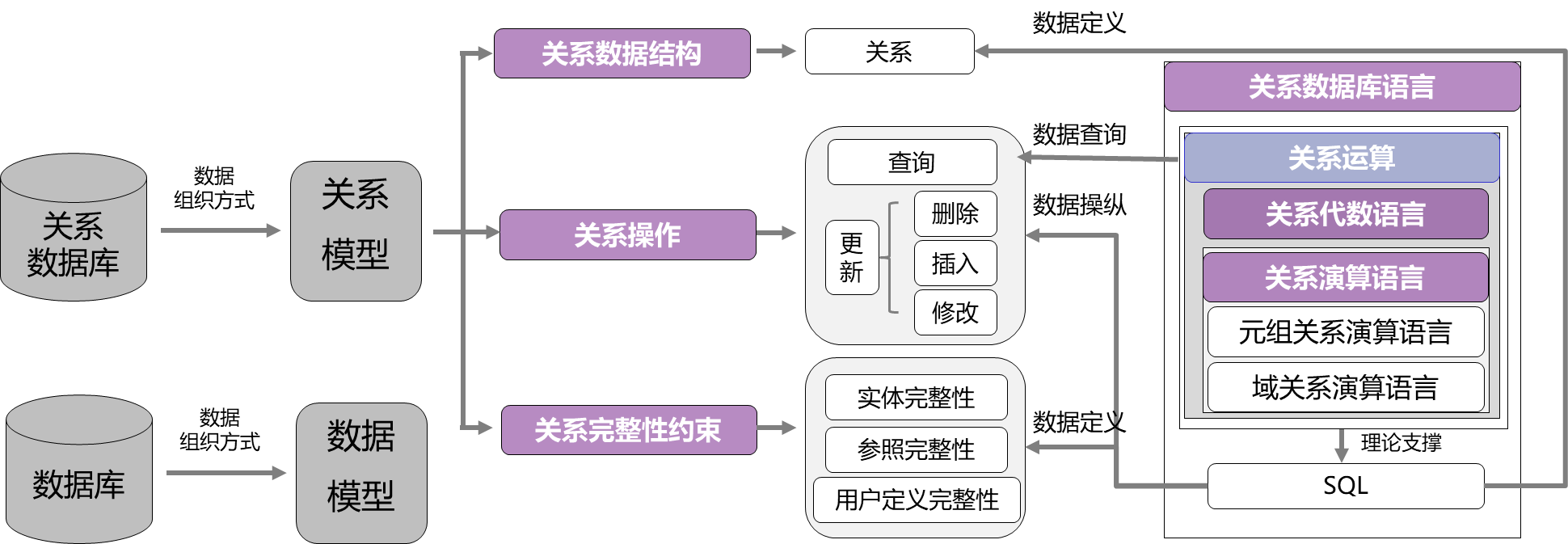
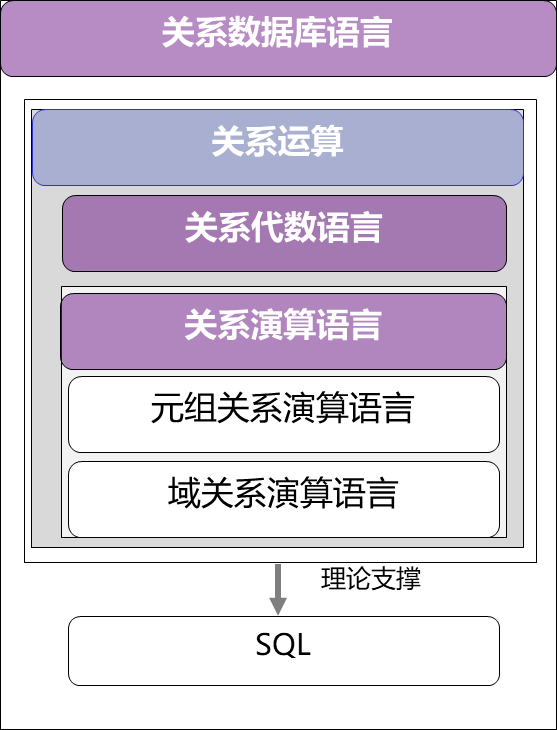
关系数据库语言
- 关系运算
- SQL
关系运算
- 关系代数
- 关系演算
- 元组关系演算
- 域关系演算
关系代数
具体在后面
关系演算
元组关系演算
元组关系演算表达式的定义为: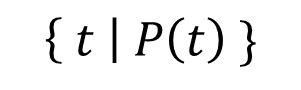
- 上述表达式返回所有使得公式P为真的元组t的集合
- P由原子公式组成,原子公式可以是以下形式之一:
- (1)t∈R,其中t是元组变量,R是关系;
- (2)t[x] Θ s[y],其中t和s是元组变量,x是t所属的关系的属性,y是s所属的关系的属性,Θ是比较运算符;
- (3)t[x] Θ c,其中t,x,Θ同上,c是属性x的域中的常量。


域关系演算


SQL
关系完整性约束
- 实体完整性约束(entity integrity constraint)
- 实体完整性约束主要是通过在关系表中实施主键取值约束,来保证关系中的每个元组可以被唯一识别。
- 如果键K是关系R的主键,则K不能取空值;
- 如果关系R的主键K是复合键,则构成复合键的多个属性均不能取空值;
- 如果键K是关系R的主键,则K的取值不能在R中重复。
- 检查规则:
- 检查关系R的主键K的值是否唯一,如果不唯一或者为空,则拒绝插入或者修改元组数据;
- 如果关系R的主键K是复合键,检查K的各个属性是否为空。如果有一个为空或者复合键不唯一,则拒绝插入或修改元组数据。
- 参照完整性约束(referential integrity constraint)
- 指代实体集之间关系的约束。被参照实体:先插入、后删除
- 删除规则:如果一个实体E(某所学校)被另一个实体F(学生)引用,可以禁止删除该实体E(学校,删除学校必须同时删除属于该学校的所有学生)。(被参照实体后删除)
- 插入规则:如果一个实体F(学生)引用了另一个实体E(学校),那么实体E(学校,学校必须已经存者学校实体集中)必须存在数据库中。(被参照实体先插入)
- 用户定义完整性约束(user-defined integrity constraint)
- 用户定义完整性约束则是用户根据具体的数据库应用场景,设置的具体的约束条件,用户定义完整性约束可以反映数据的特殊语义要求。
- 例如,在Student关系中,假设学校在录取学生的时候明确表明每位学生都必要有姓名和年龄信息,则Student关系中的Sname和Sage属性均不能取空值。
其它约束
- 非空约束
- 指关系中某一属性的取值不能为空值。
- 例如,如果对Student关系中的Sage属性增加了非空约束,则在增加一个新的学生元组的时候,其Sage属性必须要有一个非空的取值,否则数据库系统将会报错。
- 唯一约束
- 指关系中某一属性的取值不能重复的约束。
- 例如给Student关系中的Sdept属性加上唯一约束后,则表明学生的系别不能重复出现。
- 唯一约束与主键约束都可以保证关系中某一属性的取值不会重复出现。
- 不同的是,主键约束只能作用于一个关系中的一个属性且该属性的取值不能为空值,而唯一约束可以作用于一个关系中的多个属性,且该属性的取值可以为空值但不能重复。
- 自增长约束
- 一个关系中的属性取值自增长
- 默认值约束
- 一个关系中的属性的取值为默认值,例如默认值为NULL或者0
- 检查约束
- 指一个关系中的属性的取值必须满足一个指定条件的约束
- 例如,在Student关系中,Sage属性的取值范围是大于等于0
- 域约束
Chap6.1 关系代数

关系代数是一种过程化查询语言。
它包括一个运算的集合,这些运算以一个或两个关系为输入,产生一个新的关系作为结果。
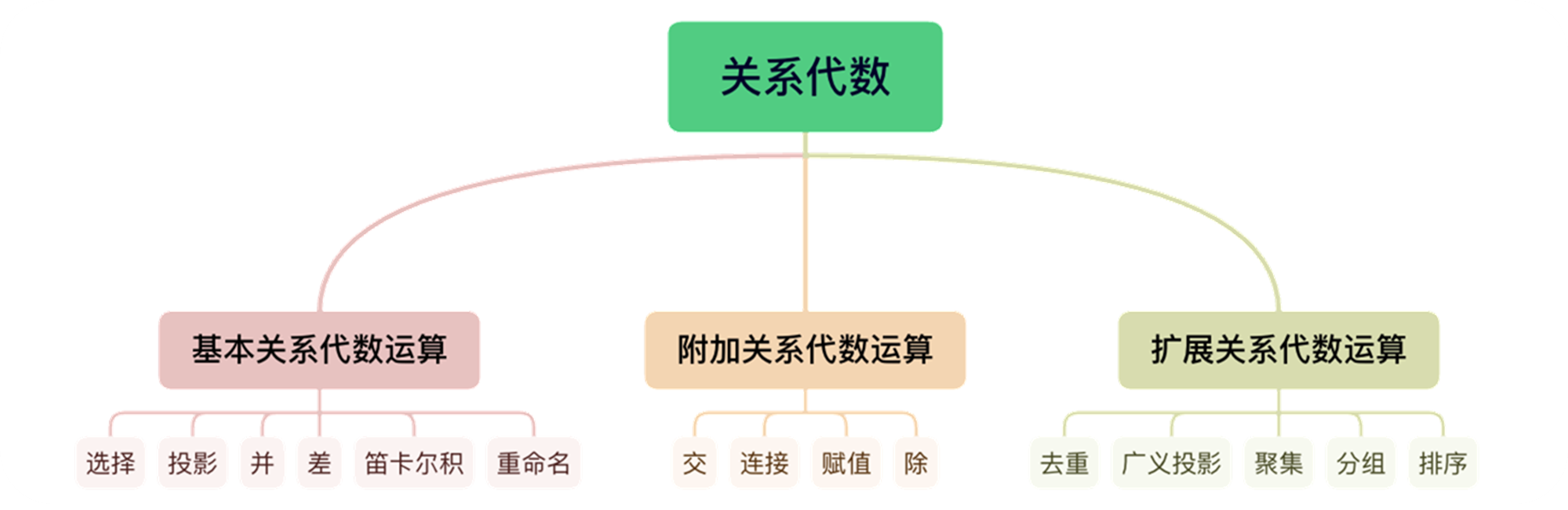
- 选择(𝜎)、投影(Π)、并(∪)、差(−)、笛卡尔积(×)、重命名(𝜌)是六种基本的关系代数运算
- 另外,交(∩)、连接(⋈)、赋值(←)、除(÷)是由基本关系代数运算组合得到的附加关系代数运算,因此这四种运算并不增加关系代数的表达能力
- 扩展关系代数运算可以实现一些使用基本关系代数运算和附加关系代数运算无法实现的功能,包括去重(𝛿)、广义投影(Π)、聚集(𝒢)、分组(𝒢)、排序(𝜏)等
6.1.1 基本运算
- 选择
- 投影
- 并
- 集合差
- 笛卡儿积
- 重命名
选择\(\sigma\)
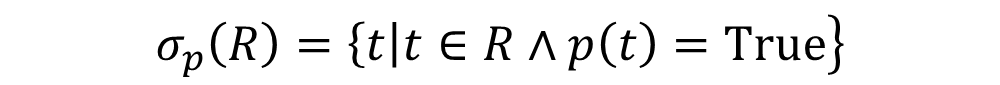
- p 为选择谓词
- p是由逻辑运算符与(⋀)、或(∨)、非(¬)连接的若干原子表达式构成的公式
- 原子表达式的形式为:X θ Y
- X,Y:属性名、常量,或者函数值
- θ:比较运算符,包括=、>、<、≥、≤、≠
例如:\(\sigma_{salary>90,000}(instructor)\)

投影\(\Pi\)
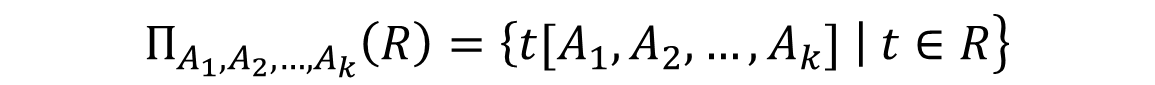
- A1,A2,…,Ak为R中的属性列
- 返回R中元组在A_1,A_2,…,A_k列上的值
- 因为关系是一个几何,所以删除重复元组(重复行)
例如:查询计算机系所有学生的学号、姓名。 \[ \Pi_{Sno,Sname}(\sigma_{Sdept="CS"}(Student)) \]
并\(\cup\)
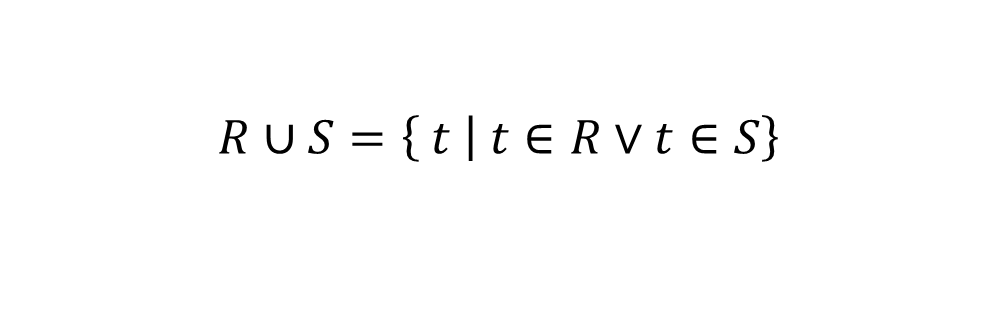
- R和S中属性个数要相同
- R和S中的属性应存在一一对应关系
- R中每个属性的域和S中对应属性的域要相同

差\(-\)
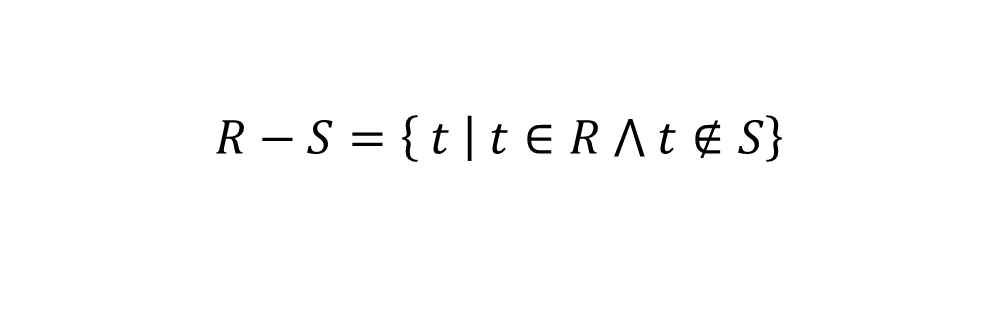
- R和S中属性个数要相同
- R和S中的属性应存在一一对应关系
- R中每个属性的域和S中对应属性的域要相同
- r-s :在r中但不在s中的元组
笛卡儿积 \(\times\)
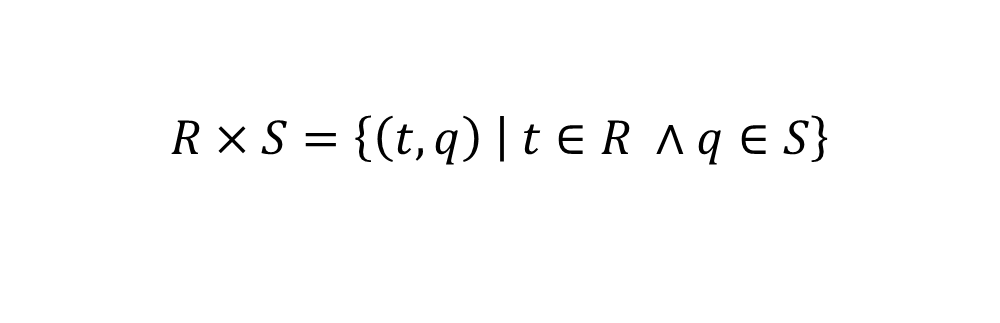
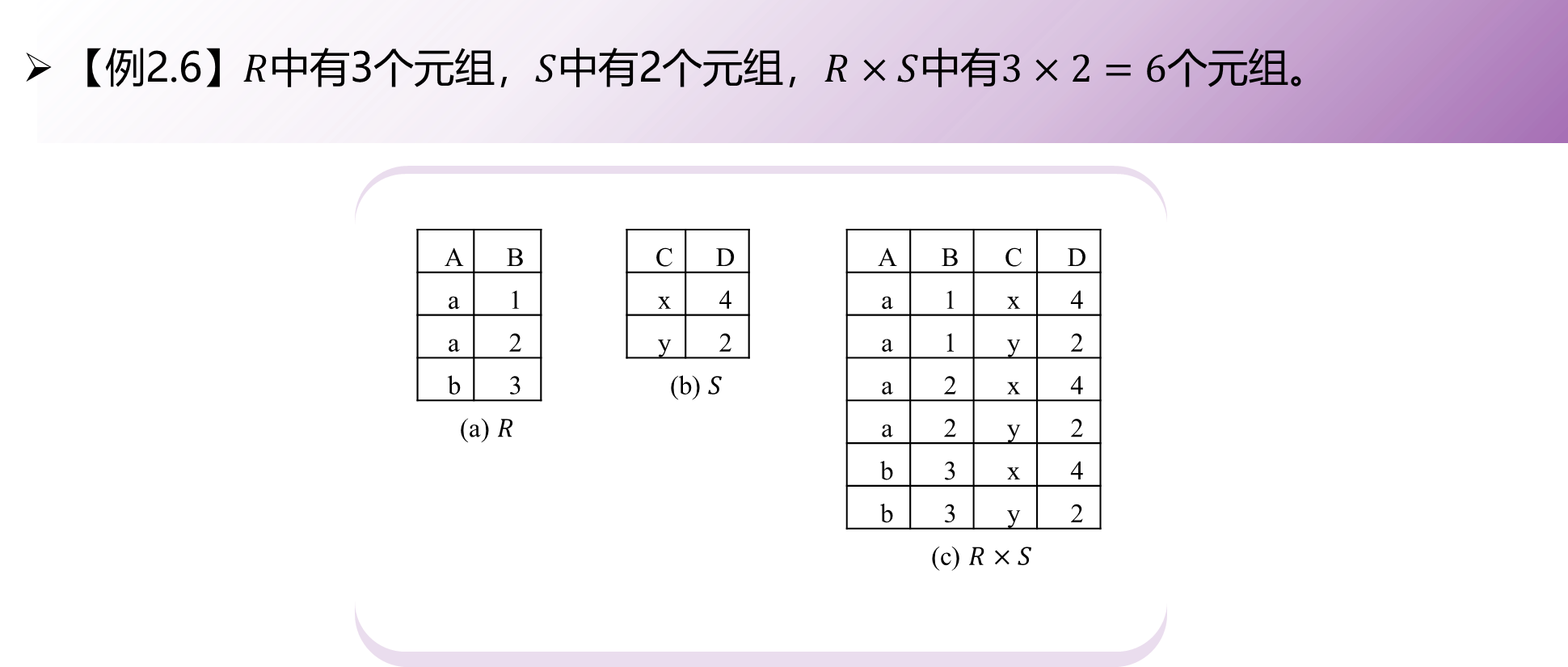
- (t,q)为R中元组t和S中元组q拼接在一起得到的元组
- R×S中有|R|×|S|个元组

重命名\(\rho\)
重命名运算(ρ)将关系R重命名为关系S:
\[ \rho_{S(A_1,A_2,A_3,\cdots,A_n)}(R) \] - 同时将各属性按照从左到右的顺序重命名为A_1,A_2,…,A_n
- \(ρ_S (R)\):只修改关系名,不修改属性名
例如,如果有一个关系$ Students(StudID, StudName, StudAge) \(,你可以使用重命名操作来将属性名修改为\) ID, Name, Age $:
$ _{(ID, Name, Age)}(Students) $这将产生一个具有属性 ( ID, Name, Age ) 的新关系,而不改变原始关系。
6.1.2 关系代数的形式化定义
6.1.3 附加的关系代数运算
- 交
- 连接
- 赋值
- 除
交\(\cap\)
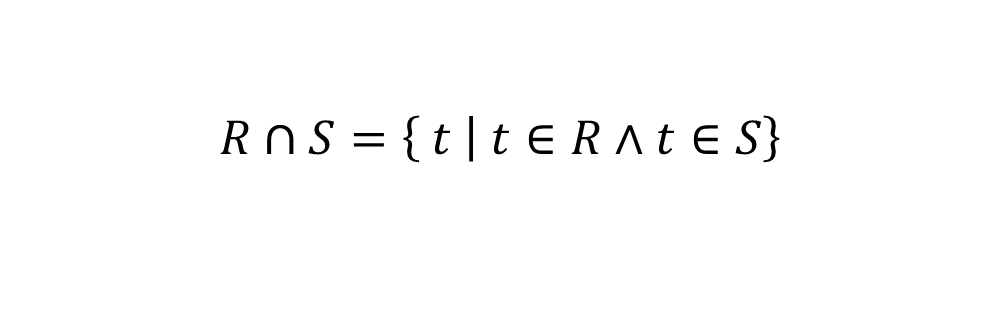
- R和S中属性个数要相同
- R和S中的属性应存在一一对应关系
- R中每个属性的域和S中对应属性的域要相同


连接\(\bowtie\)

- 外连接
- 左外连接
- 友外连接
- 全外连接
赋值\(\leftarrow\)


除\(\div\)

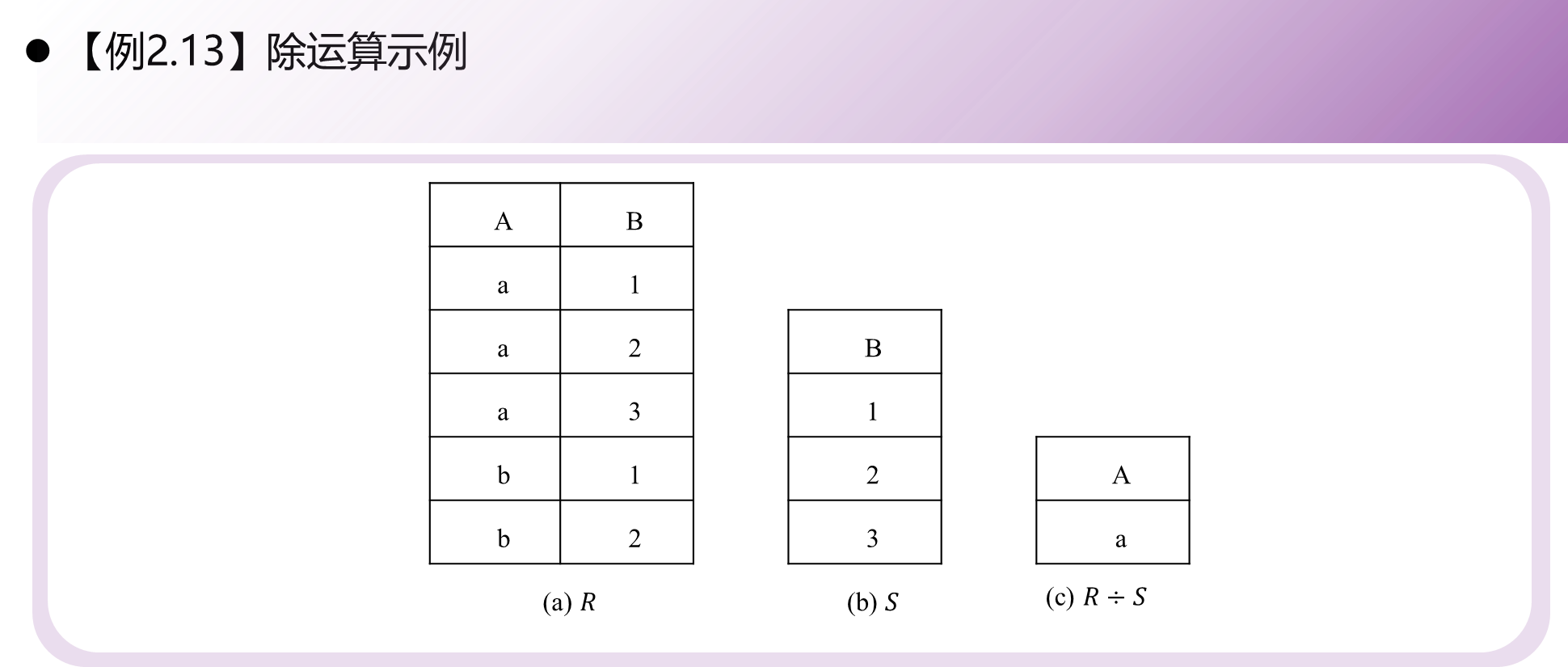
6.1.4 扩展的关系代数运算
- 去重
- 广义投影
- 聚集
- 分组
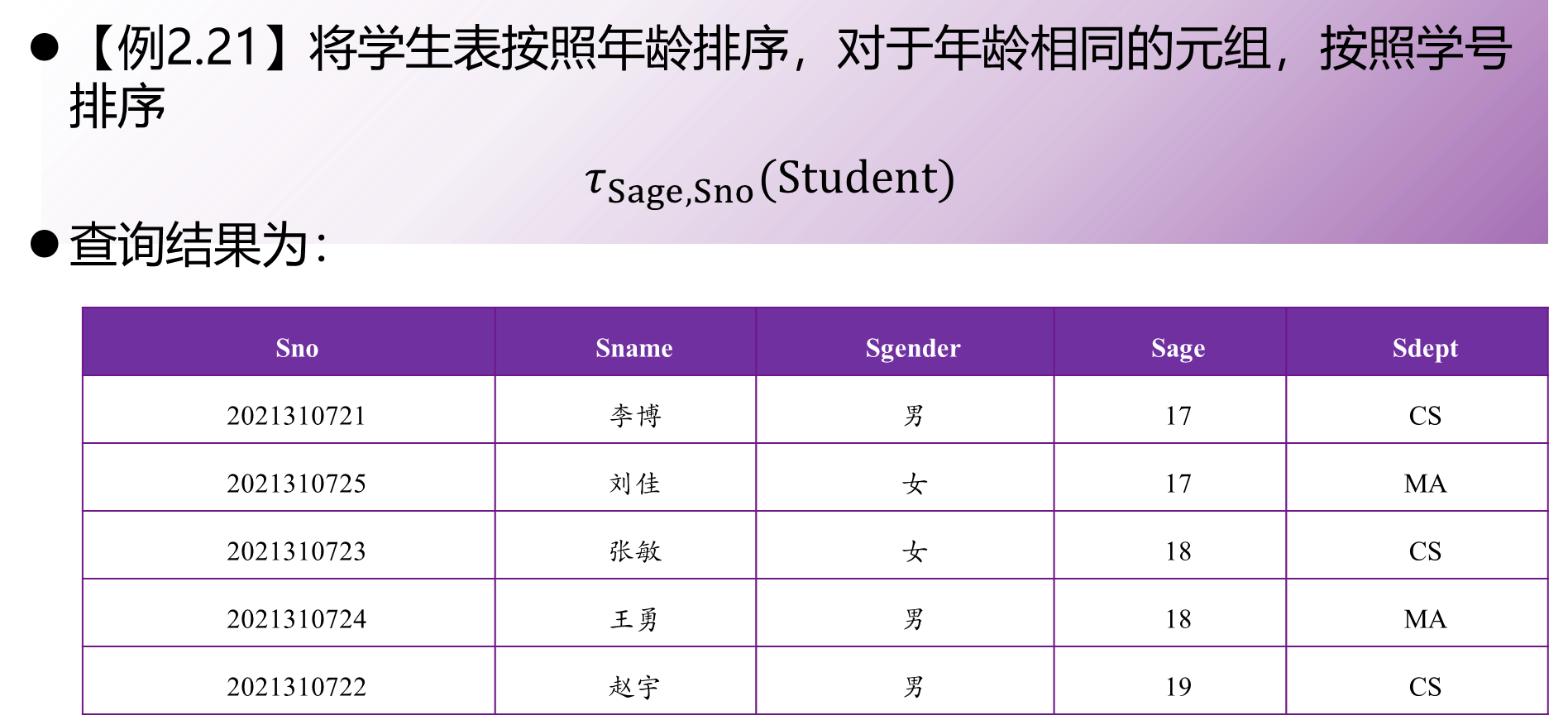
- 排序
去重\(\delta\)

广义投影\(\Pi\)
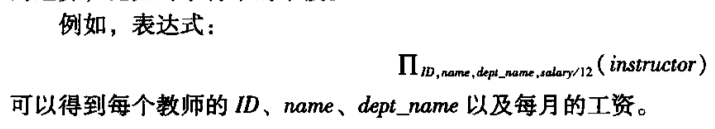

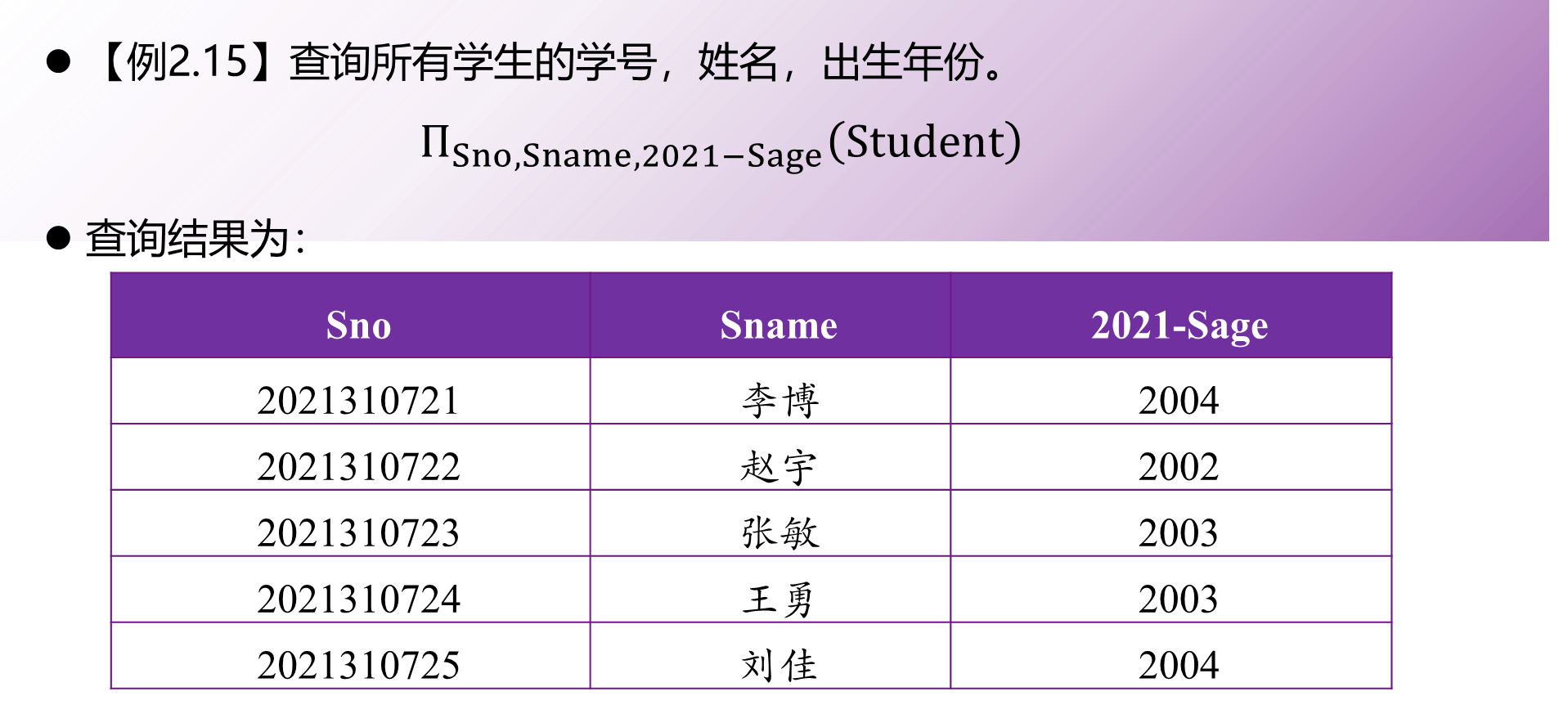
聚集\(\mathcal{G}\)



分组\(\mathcal{G}_{count\_distinct}\)


排序\(\tau\)